Personal Webpage of Dr Mathias Michel
Skip navigationNonequilibrium Quantum Thermodynamics
History of Heat Conduction Research

|

|
As one of the main topics of nonequilibrium thermodynamics, heat conduction has been of central interest for a long time. Instead of being in a global equilibrium state, the system under a heat conducting perturbation scenario enters just a local equilibrium state - defining a temperature for a macroscopically small, but microscopically large part of the system. However, there is no global temperature within the whole material defined. Being close enough to the global equilibrium, this local behavior is typically accomplished by the phenomenological proportionality of the temperature gradient ∇T and the respective energy current J within the system. The heat conductivity κ is then given by the celebrated Fourier's Law
| J = - κ ∇T . | (1) |
Since this is only a phenomenological equation the goal of all considerations on heat transport in the last decades was to find a microscopical foundation of the above formula.
The first classical attempt in this direction was done by Debye. He used the results of the kinetic gas theory for the phonons (elementary excitations of the periodic crystall) within a solid. Thinking of a phonon gas, he found that the conductivity should be proportional to the heat capacity c of the "particles", the phonon mean velocity v and free path l (the distance the phonon is able to fly until it will be scattered)
Peierls improved this approach by formulating a Boltzmann equation for the phonons to describe heat transport in solids. He was able to show that anharmonicity in the crystall potential is very important to obtain a normal heat transport, i.e., finite heat conductivity (see [Peierls1928]).
Another idea was to treat heat transport within the theory of linear response. In this context the current is the response to some external perturbation and the conductivity the respective response coefficient. In this context the coefficient is given by the famous Kubo-formula [Kubo1957]. Originally Kubo developed his theory for external electrical perturbations, e.g., contacting a wire by a battery. Nevertheless, this important theoretical progress has also been applied to other external perturbations like, e.g., heat conduction [Kubo1991, Mahan2000]. Contrary to the case of external perturbations by an electric field, thermal perturbations cannot easily be described by an potential part in the Hamiltonian of the system. The thermal perturbation is introduced by several heat baths with different temperatures coupled to the system, described by a more complicated structure than in electrodynamics. Nevertheless, instead of this insufficiencies of these approaches, such methods are often used, especially because of their tremendous success in describing non-equilibrium processes [Zotos1997, HeidrichMeisner2003, Klümper2002].
Open System Approach to Heat Conduction
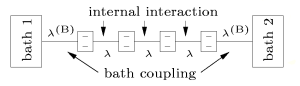 |
| Figure 2: Heat Conduction Model |
We have investigated heat transport within the theory of open quantum systems (see [Breuer2002]) , i.e., we directly couple heat baths of different temperature to the ends of a chain consisting of several two level atoms (see Figure 2). The subunits are coupled by different types of weak next neighbour interactions - a Heisenberg coupling, a XZ model (Förster coupling) as well as a random coupling.
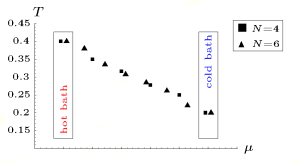 |
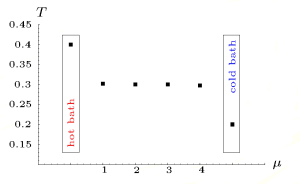 |
| Figure 3: Temperature profile for a Heisenberg chain | Figure 4: Temperature profile for a XZ model |
In these very small quantum chains, one finds a normal heat transport behavior [Saito2002, Michel2003] in almost all cases. This means that we get a non-vanishing temperature gradient within the system and therefore a finite heat conductivity from Fouriers' Law (1). This finite temperature gradient can be found for the Heisenberg (see Figure 3) as well as all randomly coupled model systems. There is only one exception the XZ model (see Figure 4) where the temperature gradient vanishes. In the case of a vanishing gradient the conductivity itself diverges (see (1)) and we the transport turns ballistic (see [Michel2003]).
Perturbation Theory in Liouville Space
Since the thermal perturbation introduced by the heat baths cannot be written as a potential part into the Hamiltonian as argued before, but as a Liouville operator for the open system, there was an attempt to consider such scenarios within the Liouville space instead of the Hilbert space [Michel2004]. This is a perturbation theory of the system due to the heat baths on both ends. We start with an unperturbed system in global equilibrium due to a coupling of two heat baths with the same temperature at both ends of the chain (see Figure 2). The perturbation enters via two heat baths with a small but finite temperature gradient. Following the ideas of Kubo by investigating electric conduction in insulators, but now on the higher level of Liouville space, one can find a similar result like in former attemps. The heat conductivity is then only dependent on the eigenstates of the unperturbed Liouville operator. The perturbation only enters as the temperature difference of the two bath systems. Since all these results are defined on the open system in Liouville space and not in the Hilbert space this approach is free from foundationary problems.
Quantum Thermodynamical Approach to Heat Conduction
Recently another approach to heat conduction in small quantum systems was suggested. It starts at quantum thermodynamics especially at the theory of relaxation to equilibrium (see Quantum Thermodynamics). If energy is located at the beginning in one part of the system, energy currents appear to destribute energy over the whole system while approaching an equilibrium state. Those currents should only be adjusted by the conductivity of the system itself. As far as an exponential decay process from a nonequilibrium state into the global equilibrium of the system takes place, one can show that the conductivity due to Fourier's Law (1) is a material constant. Therefore it is possible to account for the conductivity by observing the decay of the system into equilibrium, with no further couplings to any heat baths.
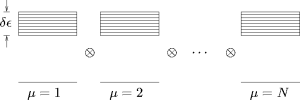 |
| Figure 5: Quantum thermodynamical heat conduction model. |
A typical quantum heat conduction model is shown in Figure 5. The total system consists of several subsystems with a special local spectrum (one ground state, and a band of exited states equally distributed over an energy interval). The subsystems couple to each other by a random energy exchanging interaction. We integrate the Schrödinger equation of the full system, only. Therefore we start with an exitation only in the first system, observing the decay to the global equilibrium state (equipartition of energy). As can be seen from Figure 6 the complete solution of the Schrödinger equation is in perfect agreement with the theoretical prediction by a Hilbert space average theory. Thus, we indeed find a normal heat conduction behavior in such small quantum systems.
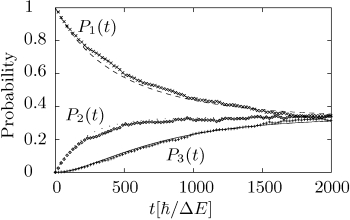 |
| Figure 6: Probability to find the exitation in one of the three subunits. Solution of the full Schrödinger equation (dots) against Hilbert Space Average Theory (lines). For details see [Michel2005]. |
This is the first hint for statistical behavior from quantum mechanics containing no further assumptions. With the help of the derived rate equation it is thus possible to find a microscopic formula for the heat conductivity, depending only on the parameters of the system (in principle the Hamiltonian). Therefore this theoretical approach could be seen as a microscopic derivation of Fourier's Law as introduced above. For details see [Michel2006].