Personal Webpage of Dr Mathias Michel
Skip navigationEquilibrium Quantum Thermodynamics
A Quantum Approach to Thermodynamics
A long known problem of thermodynamics is the foundation on an underlaying theory which is time reversible and therefore not able to show irreversible behavior. Great efforts have been made to found thermodynamics on classical Hamiltonian dynamics by Boltzmann, Gibbs etc. [Boltzmann1964, Gibbs1974] not without a great variety of additional assumption like e.g. ergodicity, molecular chaos. Recently there was an attempt to found thermodynamics onto the basis of quantum mechanics and indeed there are strong indications of thermodynamical behavior in bipartite closed quantum systems, described by pure Schrödinger dynamics (see [Borowski2003]). The main difference of this quantum mechanical approach to the classical ones is mainly the formation of entanglement between system and environment. A further great advantage is the fact that the entropy definition in quantum mechanics (von Neumann entropy) is defined for any state not only for equilibrium states. Therefore it is possible to consider entropy as a landscape over the Hilbert space. This landscape of the von Neumann entropy is for a special class of systems (thermodynamical systems: consisting of the "system" and an environment, which of course should be much larger than the system itself) nothing else than a very large highland filling almost the complete accessible part of the Hilbert space. Thus, for topological reasons one finds that almost all reachable states of the small system are states with approximately maximum entropy (see [Gemmer2001, Gemmer2004]). Accordingly, the system will evolve into an equilibrium state with maximum entropy, despite of its time-reversible Schrödinger dynamics under no further assumptions.
This is not only a new sight of the foundation of thermodynamics - irreversible behavior of a system described by reversible microscopical dynamics - but also the possibility to find thermodynamical behavior for very small systems. Furthermore the approach does not depend on any further assumption like ergodicity, molecular chaos etc. as classical attempts do.
To learn more about this quantum mechanical approach to thermodynamics see our book Quantum Thermodynamics (Springer 2004) or the informative homepage of Jochen Gemmer as well as the primary references given above.
The Way to Equilibrium
 |
|
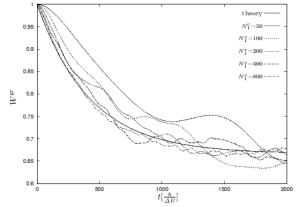
| Figure 1: Model system to investigate the decay into the equilibrium state. | Figure 2: Decay behavior of the system at the right hand side for different sizes of the environment. |
How does the system decays from an initial state of very low entropy into the above described final equilibrium state with maximum entropy? As often mentioned this decay should be an exponential decay. If one could find such an exponential decay the complicated dynamics after Schrödinger of the full system can be replaced by a simple rate equation for the considered system. Indeed, it is possible to find this exponential behavior in a very simple model system, a two level system coupled weakly to an environment consisting of two bands with a couple of levels (see Figure 1, [Gemmer2004, Gemmer2005, Gemmer2006]). The bands have the same width, but a different number of levels. The coupling between system and environment should be weak compared to the local energy of the two level system. By only solving the Schrödinger equation of this system we find an exponential decay into the expected equilibrium state (see Figure 2) which gets better for increasing size of the einvironment.
The respective rate equation describing this decay could be derived by the new "Hilbert Space Average Mathod" (HAM see Quantum Thermodynamics (Springer 2004)) or by an extension of the famous time-convolutionless (TCL) method (see [Breuer2006]), a method to derive quantum master equations.