To solve ordinary differential equations (ODE), i.e. systems of differential equations of first order Octave provides a powerful solver. The differential equations are of the type
A sub class of those ODE is a system of time-independent linear differential equation of first order which can be written as
where A is a constant matrix.
The solver is based on some fortran routines but encapsulated in a C++ class structure. The two most important classes are the class ODEFunc and the class LSODE which is a child of the first one. To use the solver the user must provide a function which computes the right hand side of his differential equation. This is equivalent to what has to be done on the Octave or Matlab command line interpreter for solving differential equations. The function computing the right hand side of the ODE has to be of the type
ColumnVector f (const ColumnVector& y, double t)
and has to return the vector
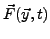 or
A
or
A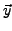 .
.
After defining this function a function pointer to it is passed to the class ODEFunc which initializes the solver. In a second step the LSODE class is used to initialize the initial state and other important parameters of the computation. Before presenting some useful functions of LSODE find a little example of the solution of a linear differential equation in the following.
#include <iostream>
#include <octave/config.h>
#include <octave/Matrix.h>
#include <octave/LSODE.h>
Matrix A;
// function computing the right hand side
ColumnVector f(const ColumnVector& y, double t)
{
// initialization of the data objects
ColumnVector dy;
int dim = A.rows();
dy = ColumnVector(dim);
// computation of dy
dy = A*y;
return dy;
}
int main()
{
// initialization of the matrix
A = Matrix(2,2);
A(0,0)=1;
A(0,1)=2;
A(1,0)=-4;
A(1,1)=-3;
// initial state
ColumnVector yi(2);
yi(0)=0.0;
yi(1)=1.0;
// vector of times at which we like to have the result
ColumnVector t(11);
for(int i=0; i<=10; i++) t(i)=0.1*i;
// container for the data
Matrix y;
Matrix dat_m(11,3);
// initialize the solver by transfering the function f
ODEFunc odef (f);
// initialize the solver with yi and the initial time
// as well as the ODEFunc object ode
LSODE ls(yi, 0.0, odef);
// compute the data
y = ls.do_integrate(t);
// put data to container together with the times
dat_m.insert(t,0,0);
dat_m.insert(y,0,1);
// output on std
std::cout << dat_m << std::endl;
return 0;
}
0 0 1
0.1 0.179763 0.707037
0.2 0.318829 0.435272
0.3 0.418297 0.193126
0.4 0.480858 -0.0138417
0.5 0.510378 -0.182668
0.6 0.511514 -0.312648
0.7 0.48936 -0.404957
0.8 0.449138 -0.462258
0.9 0.395937 -0.48831
1 0.334512 -0.487604
As can be seen the main programm uses both important classes to initialize the ODE solver. Firstly the user defined function f for the right hand side is passed to the ODEFunc class by calling its constructor
ODEFunc (ColumnVector (*f) (const ColumnVector&, double))
Secondly the class LSODE is initialized by
LSODE (const ColumnVector yi, double t, const ODEFunc& f)
Here the initial state yi and the initial time is passsed to the solver as well as the object of the class ODEFunc containing the pointer to our function f. The computation of several data points is then done by the member function do_integrate(ColumnVector t).
For very large systems of linear differential equations it is useful to encapsulate the whole computation in a class. This also avoids to define a large matrix as a global variable. We needed this to make the matrix elements accessible from inside the function f without changing its parameter set. Since the prototype of the function f is already defined by the class ODEFunc its type cannot simply be changed. Furthermore our function f cannot be simply defined as static within our class, since it uses some non-static variables namely the matrix A. This, however, makes it impossible to define a pointer to the function f which is against C++ rules.
In the following we will use a static wrapper function approach with a global pointer to the present object of our class. From within the wrapper function we can call the non-static member function f of the class object.
For more information on function pointers and how to implement a callback to a non-static member function see the very nice tutorial at newty.de.
#ifndef _LINODE_H_
#define _LINODE_H_
#include <iostream>
#include <octave/oct.h>
#include <octave/oct-rand.h>
#include <octave/config.h>
#include <octave/Matrix.h>
#include <octave/LSODE.h>
class LinODE
{
Matrix A;
public:
LinODE () {}
// constructor used to initiallize the matrix
LinODE (Matrix &matrix) {A = matrix;}
~LinODE () {}
// again the function f
ColumnVector f (const ColumnVector& y, double t);
// compute the time evolution
void compute_time_evolution (ColumnVector istate, double tint,
double tend, double deltat);
// wrapper function to pass the function f to the octave
static ColumnVector wrapper (const ColumnVector& y, double t);
};
#endif
#include "LinODE.h"
/// Global pointer to the present object for the wrapper function
void* pt2object;
// function computing the right hand side
ColumnVector LinODE::f(const ColumnVector& y, double t)
{
ColumnVector dy;
int dim = A.rows();
dy = ColumnVector(dim);
dy = A*y;
return dy;
}
void LinODE::compute_time_evolution (ColumnVector istate,
double tinit, double tend, double deltat)
{
ColumnVector t(11);
int tstep = int((tend - tinit)/deltat);
for(int i=0; i<=tstep; i++) t(i)=tinit + deltat*i;
Matrix y;
Matrix dat_m(11,3);
ODEFunc odef (wrapper);
LSODE ls (istate, tinit, odef);
y = ls.do_integrate(t);
dat_m.insert(t,0,0);
dat_m.insert(y,0,1);
std::cout << dat_m << std::endl;
}
ColumnVector LinODE::wrapper (const ColumnVector& y, double t)
{
// pointer to present object
LinODE* mySelf = (LinODE*) pt2object;
// return objects function f
return mySelf->f(y, t);
}
#include <iostream>
#include <octave/config.h>
#include <octave/Matrix.h>
#include <octave/LSODE.h>
#include "LinODE.h"
extern void* pt2object;
int main()
{
// initialization of the matrix
Matrix A = Matrix(2,2);
A(0,0)=1;
A(0,1)=2;
A(1,0)=-4;
A(1,1)=-3;
// initial state
ColumnVector yi = ColumnVector(2);
yi(0)=0.0;
yi(1)=1.0;
// generate object ode
LinODE ode = LinODE(A);
// initialize global pointer to this object
pt2object = (void*) &ode;
// compute the time evolution
ode.compute_time_evolution (yi,0,1,0.1);
return 0;
}
The result of the computation should be the same as before.
The central class LSODE is also a child of the class LSODE_options. From this one it inherits a lot of functions as well. Let us just give some of the accessible functions here
// integrate the ODE for a time t and return the state
ColumnVector do_integrate (double t)
// integrate the ODE and return a list of states at the times in the vector tout
Matrix do_integrate (const ColumnVector &tout)
// set the function computing the right hand side
ODEFunc & set_function (ODERHSFunc f)
You can find all other functions again in the respective header files LSODE.h, ODEFunc.h and LSODE_options or also at the already mentioned doxygen documentary at octave.sourceforge.net/doxygen
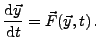
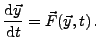
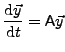
![]() or
A
or
A![]() .
.