There are several classes providing functianallity for matrices.
The most important classes are defined in dMatrix.h (real matrices) and in CMatrix.h (complex matrices).
The class for normal matrices is called Matrix and for complex ones ComplexMatrix.
Furthermore one can use two classes for diagonal matrices DiagMatrix and the in case of complex matrieces ComplexDiagMatrix.
Since all classes contain a great amount of different functions, we concentrate on the most important ones in the following.
All further information can be extracted from the header files directly or from the not very detailed octave doxygen documentation which can be found at
octave.sourceforge.net/doxygen
The two classes Matrix and ComplexMatrix provide the user with several different constructors, we just present a usefull subset of all of those:
// standard constructor of the class Matrix
Matrix (void)
// constructor to generate an object Matrix with r rows and c columns
Matrix (int r, int c)
// constructor to generate an object Matrix with r rows and c columns
// and fill it with the real value val
Matrix (int r, int c, double val)
// standard constructor of the class ComplexMatrix
ComplexMatrix (void)
// constructor to generate a ComplexMatrix with r rows and c columns
ComplexMatrix (int r, int c)
// constructor to generate a ComplexMatrix with r rows and c columns
// filled with the Complex value val
ComplexMatrix (int r, int c, const Complex& val)
Find a simple example for the definition and initialization of a 2
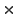2 complex matrix in the following code.
ComplexMatrix matrix;
matrix = ComplexMatrix (2, 2);
for(int r=0; r<2; r++)
{
for(int c=0; c<2; c++)
{
matrix (r, c) = Complex (r+1, c+1);
}
}
std::cout « matrix « std::endl;
(1,1) (1,2)
(2,1) (2,2)
Note that it is very easy to put the Octave objects to the standard output as done in the last line of the above code example.
Octave defines its one output rules to the standard output std.
Each element can be put to std or into a file by using just the standard commands, i.e., std::cout << followed by the name of the data structure.
(Note that there is a problem with using the namespace std see 5.)
Further constructors for diagonal matrices are difined as shown in the following.
Here we discuss those for real matrices only, even if the same type of expressions excist also for all complex matrix classes.
// standard constructor of the class Matrix
DiagMatrix (void)
// constructor to generate a Matrix with r rows and c columns
DiagMatrix (int r, int c)
// constructor to generate a Matrix, RowVector first diagonal
DiagMatrix (const RowVector& a)
// constructor to generate a Matrix, ColumnVector first diagonal
DiagMatrix (const ColumnVector& a)
Objects of the two diagonal classes can be transformed into their basic class by using
// generating a Matrix from a
Matrix (const DiagMatrix &a)
// generating a ComplexMatrix from a
ComplexMatrix (const ComplexDiagMatrix &a)
After you have build an instance of any of the above introduced classes, Octave provides you with lot of tools to manipulate those objects. To account for the size of a matrix (normal as well as complex) one can use the member functions
// number of rows
int row (void)
// number of columns
int column (void)
The transposed and the inverse matrix can be computed using
// transpose the matrix
Matrix transpose (void)
// invert the matrix
Matrix inverse (void)
Additionally for complex matrices there is a function which conjugates each entry and one which adjoints the matrix
// conjugate the elements
ComplexMatrix conj (const ComplexMatrix& a)
// adjoint the matrix
ComplexMatrix hermitian (void)
In the following example we show how to use some of these functions. Therefore we define the same matrix as before in the above example.
ComplexMatrix matrix;
int r, c;
...
std::cout « matrix;
// dimension of the matrix
r = matrix.rows();
c = matrix.cols();
std::cout « "dimensions of the matrix:";
std::cout « r « "x" « c « endl;
// transpose matrix
std::cout « matrix.transpose();
std::cout « matrix.hermitian();
(1,1) (1,2)
(2,1) (2,2)
dimensions of the matrix: 2x2
(1,1) (2,1)
(1,2) (2,2)
(1,-1) (2,-1)
(1,-2) (2,-2)
Functions for extracting parts of a matrix:
// extract the ith row of a matrix
RowVector row (int i)
// extract the ith column of a matrix
ColumnVector column (int i)
// extract the ith row of a complex matrix
ComplexRowVector row (int i)
// extract the ith column of a complex matrix
ComplexColumnVector column (int i)
// extract the diagonal of a matrix
ColumnVector diag (void)
// extract the diagonal of a complex matrix
ComplexColumnVector diag (void)
// extract a submatrix with upper left corner at the elements
// r1 and c1 and the bottem right corner at r2 c2
ComplexMatrix extract (int r1, int c1, int r2, int c2)
// extract a submatrix with upper left corner at the elements
// r1 and c1 and nr rows and nc columns
ComplexMatrix extract_n (int r1, int c1, int nr, int nc)
Most mathematical operators +, -, *, operators as +=, -= as well as comparison operators ==, != are defined.
This means that you can mostly use these operators without any further definition of functions and they operate intuitively.
For example
Matrix a_matrix, b_matrix, c_matrix;
// definition of size and setting of entries
...
c_matrix = a_matrix + b_matrix;