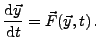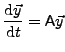Personal Webpage of Dr Mathias Michel

Skip navigation

Howto Use Octave Functions in C++ Programs





Getting Started


Octave is a very nice free Matlab clone and provides many helpful mathematical functions. Especially linear algebra calculations are rather easy, but Octave comes also with lot more. For more information and to download octave see the homepage of the project at www.gnu.org/software/octave/. To use the very powerful Octave functions in your C/C++ programs include the main octave header file


#include <octave/oct.h>

which is mostly located in \usr\local\include\octave-version-number Mostly, it will not be necessary to include further header files, since this file already includes most of the octave functions. Nevertheless we will refer to the respective special headers in the following to give you the chance to gain some further information.


To compile your C/C++ code, e.g. with g++, set the -I option of your compiler to the location of the octave include files. For the linking process octave provides you with a very useful make file mkoctfile. Standardly this make file is also used for translating octave code into .oct files. It comes with the option --link-stand-alone which produces an executable file of your C/C++ program containing octave subroutines. The following Makefile represents a simple example to compile and link your program called test at the end:


Makefile


makefile:
all: test

clean:
     -rm test.o test

test: test.o
     mkoctfile --link-stand-alone -o test test.o

test.o: main.cpp
     g++ -c -I$(OCTAVE_INCLUDE) -I$(OCTAVE_INCLUDE)octave -o test.o main.cpp

Please note that the spaces before the commands must be a tabulator character according to standard rules of Makefiles. The environment variable $OCTAVE_INCLUDE should be set to your octave include path, which could be, e.g., /usr/include/octave-2.1.73. By using the command make all your program will be compiled and linked.





Complex Numbers


Octave defines its own complex data structure in the header oct-cmplx.h. The programmers propose: " By using this file instead of `complex.h', we can easily avoid buggy implementations of the standard complex data type (if needed)." Thus the data structure is defined as


typedef std::complex<double> Complex

To define a complex number, e.g. 0.7+0.3i, within your program use


Complex number = Complex (0.7, 0.3);

The following useful functions are available to manipulate the above given complex data structure.


// real part
double real (const Complex& z)
// imaginary part
double imag (const Complex& z)
// absolute value
double abs (const Complex& z)
// argument of the complex number
double arg (const Complex& z)
// complex conjugate complex number
Complex conj (const Complex& z)
// complex exponential function
Complex exp (const Complex& z)
// power n of a complex number
Complex pow (const Complex& z, int n)
// square root of a complex number
Complex sqrt (const Complex& z)




The Matrix Classes


There are several classes providing functianallity for matrices. The most important classes are defined in dMatrix.h (real matrices) and in CMatrix.h (complex matrices). The class for normal matrices is called Matrix and for complex ones ComplexMatrix. Furthermore one can use two classes for diagonal matrices DiagMatrix and the in case of complex matrieces ComplexDiagMatrix.


Since all classes contain a great amount of different functions, we concentrate on the most important ones in the following. All further information can be extracted from the header files directly or from the not very detailed octave doxygen documentation which can be found at octave.sourceforge.net/doxygen The two classes Matrix and ComplexMatrix provide the user with several different constructors, we just present a usefull subset of all of those:


// standard constructor of the class Matrix
Matrix (void)
// constructor to generate an object Matrix with r rows and c columns
Matrix (int r, int c)
// constructor to generate an object Matrix with r rows and c columns
// and fill it with the real value val
Matrix (int r, int c, double val)
// standard constructor of the class ComplexMatrix
ComplexMatrix (void)
// constructor to generate a ComplexMatrix with r rows and c columns
ComplexMatrix (int r, int c)
// constructor to generate a ComplexMatrix with r rows and c columns
// filled with the Complex value val
ComplexMatrix (int r, int c, const Complex& val)

Find a simple example for the definition and initialization of a 2 $ \times$ 2 complex matrix in the following code.


Generate a Complex Matrix (Code)


ComplexMatrix matrix;
matrix = ComplexMatrix (2, 2);
for(int r=0; r<2; r++)
  {
    for(int c=0; c<2; c++)
      {
        matrix (r, c) = Complex (r+1, c+1);
      }
  }
std::cout « matrix « std::endl;

Generate a Complex Matrix (Output)


(1,1) (1,2)
(2,1) (2,2)

Note that it is very easy to put the Octave objects to the standard output as done in the last line of the above code example. Octave defines its one output rules to the standard output std. Each element can be put to std or into a file by using just the standard commands, i.e., std::cout << followed by the name of the data structure. (Note that there is a problem with using the namespace std see 5.)


Further constructors for diagonal matrices are difined as shown in the following. Here we discuss those for real matrices only, even if the same type of expressions excist also for all complex matrix classes.


// standard constructor of the class Matrix
DiagMatrix (void)
// constructor to generate a Matrix with r rows and c columns
DiagMatrix (int r, int c)
// constructor to generate a Matrix, RowVector first diagonal
DiagMatrix (const RowVector& a)
// constructor to generate a Matrix, ColumnVector first diagonal
DiagMatrix (const ColumnVector& a)

Objects of the two diagonal classes can be transformed into their basic class by using

// generating a Matrix from a
Matrix (const DiagMatrix &a)
// generating a ComplexMatrix from a
ComplexMatrix (const ComplexDiagMatrix &a)

After you have build an instance of any of the above introduced classes, Octave provides you with lot of tools to manipulate those objects. To account for the size of a matrix (normal as well as complex) one can use the member functions


// number of rows
int row (void)
// number of columns
int column (void)

The transposed and the inverse matrix can be computed using


// transpose the matrix
Matrix transpose (void)
// invert the matrix
Matrix inverse (void)

Additionally for complex matrices there is a function which conjugates each entry and one which adjoints the matrix


// conjugate the elements
ComplexMatrix conj (const ComplexMatrix& a)
// adjoint the matrix
ComplexMatrix hermitian (void)

In the following example we show how to use some of these functions. Therefore we define the same matrix as before in the above example.


Linear Algebra (Code)


ComplexMatrix matrix;
int r, c;
...
std::cout « matrix;
// dimension of the matrix
r = matrix.rows();
c = matrix.cols();
std::cout « "dimensions of the matrix:";
std::cout « r « "x" « c « endl;
// transpose matrix
std::cout « matrix.transpose();
std::cout « matrix.hermitian();

Linear Algebra (Output)


(1,1) (1,2)
(2,1) (2,2)

dimensions of the matrix: 2x2

(1,1) (2,1)
(1,2) (2,2)

(1,-1) (2,-1)
(1,-2) (2,-2)

Functions for extracting parts of a matrix:


// extract the ith row of a matrix
RowVector row (int i)
// extract the ith column of a matrix
ColumnVector column (int i)
// extract the ith row of a complex matrix
ComplexRowVector row (int i)
// extract the ith column of a complex matrix
ComplexColumnVector column (int i)
// extract the diagonal of a matrix
ColumnVector diag (void)
// extract the diagonal of a complex matrix
ComplexColumnVector diag (void)
// extract a submatrix with upper left corner at the elements
// r1 and c1 and the bottem right corner at r2 c2
ComplexMatrix extract (int r1, int c1, int r2, int c2)
// extract a submatrix with upper left corner at the elements
// r1 and c1 and nr rows and nc columns
ComplexMatrix extract_n (int r1, int c1, int nr, int nc)

Most mathematical operators +, -, *, operators as +=, -= as well as comparison operators ==, != are defined. This means that you can mostly use these operators without any further definition of functions and they operate intuitively. For example


Matrix a_matrix, b_matrix, c_matrix;
// definition of size and setting of entries
...
c_matrix = a_matrix + b_matrix;




Eigensystem


Very important is the EIG class, computing the eigenvalues and eigenvectors of all the above defined different matrix classes. By calling the constructor


// eigensystem of Matrix a
EIG (const Matrix& a)
// eigensystem of ComplexMatrix a
EIG (const ComplexMatrix& a)

the eigensystem of the matrix will be computed and stored within the class. The two functions


// returns the eigenvalues as a ComplexColumnVector
ComplexColumnVector eigenvalues (void)
// returns the eigenvectors in the columns of a ComplexMatrix
ComplexMatrix eigenvectors (void)

return the eigenvalues as a ComplexColumnVector and the eigenvectors oin the columns of a ComplexMatrix.


Eigensystem Example (Code)


#include <iostream>
#include <octave/oct.h>

int main()
{
     // initialization of the matrix
     ComplexMatrix A = ComplexMatrix(2,2);
     A(0,0)=Complex(1,1);A(0,1)=Complex(1,2);
     A(1,0)=Complex(2,1);A(1,1)=Complex(2,2);

     // compute eigensystem of A
     EIG eig = EIG(A);

     // eigenvalues
     std::cout « "eigenvalues:" « std::endl;
     std::cout « eig.eigenvalues();

     // eigenvectors
     ComplexMatrix V = (eig.eigenvectors());
     std::cout « "eigenvectors:" « std::endl;
     std::cout « V;

     // transformation to eigensystem of A
     ComplexMatrix D = ComplexMatrix(2,2);
     D = V.inverse()*A*V;
     std::cout « "diagonal matrix" « std::endl;
     std::cout « D;

     return 0;
}

Eigensystem Example (Output)


eigenvalues:
(-0.158312,-0.158312)
(3.15831,3.15831)
eigenvectors:
 (0.806694,0) (0.560642,0.186881)
 (-0.560642,0.186881) (0.806694,0)
diagonal matrix
 (-0.158312,-0.158312) (-5.13478e-16,2.77556e-17)
 (-4.44089e-16,-3.33067e-16) (3.15831,3.15831)



Systems of Differential Equations


To solve ordinary differential equations (ODE), i.e. systems of differential equations of first order Octave provides a powerful solver. The differential equations are of the type


$\displaystyle \frac{\text{d}\vec{y}}{\text{d}t} = \vec{F}(\vec{y},t)\,.$    

A sub class of those ODE is a system of time-independent linear differential equation of first order which can be written as


$\displaystyle \frac{\text{d}\vec{y}}{\text{d}t} = \text{\sf A} \vec{y}$    

where A is a constant matrix.

The solver is based on some fortran routines but encapsulated in a C++ class structure. The two most important classes are the class ODEFunc and the class LSODE which is a child of the first one. To use the solver the user must provide a function which computes the right hand side of his differential equation. This is equivalent to what has to be done on the Octave or Matlab command line interpreter for solving differential equations. The function computing the right hand side of the ODE has to be of the type


ColumnVector f (const ColumnVector& y, double t)

and has to return the vector $ \vec{F}(\vec{y},t)$ or A$ \vec{y}$ .


After defining this function a function pointer to it is passed to the class ODEFunc which initializes the solver. In a second step the LSODE class is used to initialize the initial state and other important parameters of the computation. Before presenting some useful functions of LSODE find a little example of the solution of a linear differential equation in the following.


ODE Solver (Code)


#include <iostream>
#include <octave/config.h>
#include <octave/Matrix.h>
#include <octave/LSODE.h>

Matrix A;

// function computing the right hand side
ColumnVector f(const ColumnVector& y, double t)
{
     // initialization of the data objects
     ColumnVector dy;
     int dim = A.rows();
     dy = ColumnVector(dim);

     // computation of dy
     dy = A*y;
     return dy;
}

int main()
{
     // initialization of the matrix
     A = Matrix(2,2);
     A(0,0)=1;
     A(0,1)=2;
     A(1,0)=-4;
     A(1,1)=-3;

     // initial state
     ColumnVector yi(2);
     yi(0)=0.0;
     yi(1)=1.0;
     // vector of times at which we like to have the result
     ColumnVector t(11);
     for(int i=0; i<=10; i++) t(i)=0.1*i;
     // container for the data
     Matrix y;
     Matrix dat_m(11,3);

     // initialize the solver by transfering the function f
     ODEFunc odef (f);
     // initialize the solver with yi and the initial time
     // as well as the ODEFunc object ode
     LSODE ls(yi, 0.0, odef);
     // compute the data
     y = ls.do_integrate(t);

     // put data to container together with the times
     dat_m.insert(t,0,0);
     dat_m.insert(y,0,1);

     // output on std
     std::cout << dat_m << std::endl;
     return 0;
}

ODE Solver (Output)


0    0          1
0.1  0.179763   0.707037
0.2  0.318829   0.435272
0.3  0.418297   0.193126
0.4  0.480858  -0.0138417
0.5  0.510378  -0.182668
0.6  0.511514  -0.312648
0.7  0.48936   -0.404957
0.8  0.449138  -0.462258
0.9  0.395937  -0.48831
1    0.334512  -0.487604

As can be seen the main programm uses both important classes to initialize the ODE solver. Firstly the user defined function f for the right hand side is passed to the ODEFunc class by calling its constructor


ODEFunc (ColumnVector (*f) (const ColumnVector&, double))

Secondly the class LSODE is initialized by


LSODE (const ColumnVector yi, double t, const ODEFunc& f)

Here the initial state yi and the initial time is passsed to the solver as well as the object of the class ODEFunc containing the pointer to our function f. The computation of several data points is then done by the member function do_integrate(ColumnVector t).


For very large systems of linear differential equations it is useful to encapsulate the whole computation in a class. This also avoids to define a large matrix as a global variable. We needed this to make the matrix elements accessible from inside the function f without changing its parameter set. Since the prototype of the function f is already defined by the class ODEFunc its type cannot simply be changed. Furthermore our function f cannot be simply defined as static within our class, since it uses some non-static variables namely the matrix A. This, however, makes it impossible to define a pointer to the function f which is against C++ rules.


In the following we will use a static wrapper function approach with a global pointer to the present object of our class. From within the wrapper function we can call the non-static member function f of the class object. For more information on function pointers and how to implement a callback to a non-static member function see the very nice tutorial at newty.de.


LinODE.h


#ifndef _LINODE_H_
#define _LINODE_H_

#include <iostream>
#include <octave/oct.h>
#include <octave/oct-rand.h>
#include <octave/config.h>
#include <octave/Matrix.h>
#include <octave/LSODE.h>

class LinODE
{
     Matrix A;

     public:
     LinODE () {}
     // constructor used to initiallize the matrix
     LinODE (Matrix &matrix) {A = matrix;}
     ~LinODE () {}

     // again the function f
     ColumnVector f (const ColumnVector& y, double t);
     // compute the time evolution
     void compute_time_evolution (ColumnVector istate, double tint,
       double tend, double deltat);
     // wrapper function to pass the function f to the octave
     static ColumnVector wrapper (const ColumnVector& y, double t);
};

#endif

LinODE.cpp


#include "LinODE.h"

/// Global pointer to the present object for the wrapper function
void* pt2object;

// function computing the right hand side
ColumnVector LinODE::f(const ColumnVector& y, double t)
{
     ColumnVector dy;
     int dim = A.rows();
     dy = ColumnVector(dim);
     dy = A*y;
     return dy;
}

void LinODE::compute_time_evolution (ColumnVector istate,
     double tinit, double tend, double deltat)
{

     ColumnVector t(11);
     int tstep = int((tend - tinit)/deltat);
     for(int i=0; i<=tstep; i++) t(i)=tinit + deltat*i;
     Matrix y;
     Matrix dat_m(11,3);

     ODEFunc odef (wrapper);
     LSODE ls (istate, tinit, odef);
     y = ls.do_integrate(t);

     dat_m.insert(t,0,0);
     dat_m.insert(y,0,1);

     std::cout << dat_m << std::endl;
}

ColumnVector LinODE::wrapper (const ColumnVector& y, double t)
{
     // pointer to present object
     LinODE* mySelf = (LinODE*) pt2object;
     // return objects function f
     return mySelf->f(y, t);
}

Main.cpp


#include <iostream>
#include <octave/config.h>
#include <octave/Matrix.h>
#include <octave/LSODE.h>

#include "LinODE.h"

extern void* pt2object;

int main()
{
     // initialization of the matrix
     Matrix A = Matrix(2,2);
     A(0,0)=1;
     A(0,1)=2;
     A(1,0)=-4;
     A(1,1)=-3;

     // initial state
     ColumnVector yi = ColumnVector(2);
     yi(0)=0.0;
     yi(1)=1.0;

     // generate object ode
     LinODE ode = LinODE(A);
     // initialize global pointer to this object
     pt2object = (void*) &ode;
     // compute the time evolution
     ode.compute_time_evolution (yi,0,1,0.1);
     return 0;
}

The result of the computation should be the same as before.


The central class LSODE is also a child of the class LSODE_options. From this one it inherits a lot of functions as well. Let us just give some of the accessible functions here


// integrate the ODE for a time t and return the state
ColumnVector do_integrate (double t)
// integrate the ODE and return a list of states at the times in the vector tout
Matrix do_integrate (const ColumnVector &tout)
// set the function computing the right hand side
ODEFunc & set_function (ODERHSFunc f)

You can find all other functions again in the respective header files LSODE.h, ODEFunc.h and LSODE_options or also at the already mentioned doxygen documentary at octave.sourceforge.net/doxygen





Problems


I realized that there is some problem using the namespace std by adding the line to the beginning of your code


using namespace std

In this case the program will not be translated any more according to some conflicts in the Octave files. Presently, I am not shure what the reason for that problem is.





About this Tutorial


Why using Octave in your C/C++ programs?

I am using Octave in my C++ programs for quite a while. Since I was always used to program in C++, but most of the scientific mathematical libraries are in fortran, Octave was a nice possibility for me to further write C programs. Furthermore it also includes lot of the powerful fortran tools and provides thus a C++ frontend to those routines. Thus it is possible to use the functionality of Octave together with a lot of other libraries and functions in one single C++ project.


Unfortunately the documentation of how to use octave as a library is not very detailed. This made me to write down all the things I needed in the last years. Maybe there are some other people who also would like to use Octave directly in their C/C++ programs and I hope that this helps them to get started with it.


If you are indeed planning to start with using Octave please also have a look on the following helpful webpages:



If you would like to print out this manual, find a printable version in different formats following the links below:


howto-octave-c++.ps
howto-octave-c++.pdf

Furthermore it would be very kind of you to give me some feedback concerning this tutorial. Of course some errors are unavoidable on such sites. Would you please let me know if you have found some? I am also interested in tips and tricks to make things easier, further Octave functions and how to use them, or simply in if you found this homepage helpful or not. Please contact me under:


m.michel@surrey.ac.uk

Find some more information about me and further contact details on my homepage:


www.mathias-michel.de

Of course I am not able to guarantee that the small code examples work also with your system, i.e., nothing is guaranteed and you use everything at your own risk. The examples are tested with the octave version 2.1.73 and work fine at different systems even at an infiniband cluster computer. I checked the given links and hope that they work fine. However I declare that I am not responsible for the contents of those pages.


This document was generated using LaTeX2HTML
Mathias Michel 2007-07-12
Brilliant free software products:

octave.org

kdevelop.org

open-mpi.org

subversion.tigris.org

openSUSE.org

quanta.kdewebdev.org

kde.org
19th February 2008                                                                                                                                                                                                                       © Copyright 2006 by MM